阿里DIN模型
10.21总算写完了……
论文背景
论文:Deep Interesting Network for Click-Through Rate Prediction
下载地址
2018年 阿里
现有问题
目前的深度学习模型都是先将稀疏输入特征映射为低维嵌入向量,再转换为固定长度的向量,最后联结起来送入MLP。这个固定长度的向量会成为瓶颈,无法从历史行为中捕获用户不同的兴趣。因此,本文提出深度兴趣网络Deep Interest Network(DIN)。它设计了一个局部激活单元从用户历史行为中自适应学习用户兴趣。另外,本文提出了两大技术:小批量感知正则化(mini-batch aware regularization)和数据自适应激活函数(data adaptive activation function)。
关键词
点击率预测(Click-Through Rate Prediction)、展示广告(Display Advertising),线上贸易(E-commerce)
引言 INTRODUCTION
Embedding & MLP方法通过将用户行为嵌入向量转换为一个固定长度的向量来学习用户所有兴趣的表示,所有的表示向量是欧式空间。换言之,将用户不同的兴趣压缩到一个固定长度的向量,限制了表达能力。为了更好地表达用户不同兴趣,就要扩展向量长度。这会增多学习参数,并且增加过拟合的风险。也加重了计算和存储的压力,对于工业线上系统来说很困难。
另一方面,没有必要把用户全部兴趣压缩到同一个向量里,因为只有部分兴趣会影响用户下一个动作(点击或不点击)。
训练的问题:
基于SGD的优化方法只更新出现在每个小批量中的稀疏特征的参数。然而,加上传统的ℓ2正则化,计算变得不可接受,这需要为每个小批量计算整个参数的L2范数(在阿里的场景,大小按比例增加到数十亿)。本文提出了一种新的小批量正则化方法,在L2范数的计算中,每个小批量正则化中只出现非零特征参数,使得计算是可接受的。另外,设计了一个数据自适应激活函数,推广到常用的PReLU,它通过自适应地调整输入的校正点,也就是输入的分布,并被证明有助于训练具有稀疏特征的工业网络。
贡献点
- 指出了使用固定长度向量来表达用户不同兴趣的局限性,并设计了一种新的深度兴趣网络(DIN),它引入了一个局部激活单元来自适应地从给定广告的历史行为中学习用户兴趣的表示。DIN可以大大提高模型的表达能力,更好地捕捉用户兴趣的多样性特征。
- 开发了两种新的技术来帮助训练工业深度网络:I)一种小批量感知正则化器,这种正则化器在具有大量参数的深度网络上节省了大量的正则化计算,并且有助于避免过拟合;ii)一种数据自适应激活函数,这种函数通过考虑输入的分布来推广PReLU,并且表现出良好的性能。
- 在公共数据集和AI-ibaba数据集上进行了大量实验。结果验证了所提出的DIN和训练技术的有效性。所提出的方法已经在全球最大的广告平台之一阿里巴巴的商业展示广告系统中得到了应用,为业务的发展做出了重大贡献。
代码:https://github.com/zhougr1993/DeepInterestNetwork
背景 BACKGROUND

预测每个给定广告的点击率,然后选择排名最高的广告。
深度兴趣网络 DEEP INTEREST NETWORK
特征表示 Feature Representation


表中描述了我们系统中使用的全部特征集,它由四类组成,其中用户行为特征是典型的多热点编码向量,包含丰富的用户兴趣信息。注意,在我们的设置中,没有组合特性。我们利用深度神经网络捕获特征的交互作用。
基线模型 Base Model(Embedding&MLP)

嵌入层(Embedding layer)
池化层和连接层(Pooling layer and Concat layer)
得到定长向量:$e_i = pooling(e_{i_1}, e_{i_2}, …, e_{i_k})$
最常用的是sum pooling和average pooling。
MLP
Loss
$$L = - \frac{1}{N}\sum_{(x,y)∈S}(ylogp(x) + (1 - y)log(1 - p(x)))$$
S是尺寸为N的训练集,x是输入,y是标签。p(x)是经过softmax层后的输出,代表样本x被点击的概率。
DIN架构 The structure of Deep Interest Network
基线模型对一个用户使用定长向量表示,无论候选广告是什么。
为了表示用户兴趣多样化,一种简单的方法是扩展嵌入维度,但这会增加学习参数规模。有过拟合的风险,并且增加了计算和存储的负担。
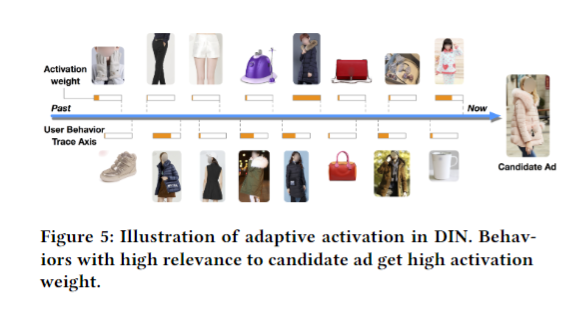
DIN模拟了关于给定广告的用户局部激活兴趣。
DIN引入了一个用于用户行为特征的局部激活单元,使用了加权求和池化(weighted sum pooling)来自适应计算当给定一个候选广告A时,用户的表示$V_U$。
局部激活单元公式:
$$v_U = f(v_A, e_1, e_2, …, e_H) = \sum_{j=1}^{H}a(e_j, v_A)e_j = \sum_{j = 1}^{H}w_je_j$$
其中,${e_1, e_2, …, e_H}$是用户U的行为嵌入向量(长度为H),$v_U(A)$是广告A的嵌入向量。
在这种方式下,$v_U(A)$在不同的广告下,a(·)是一个带有激活权重输入的前向反馈网络。除了这两部分输入嵌入向量,a(·)将它们的外积喂入后续网络。
a(·)softmax输出后的标准化被舍弃。
训练方法 TRAINING TECHNIQUES
小批量感知正则化 Mini-batch Aware Regularization
工业训练网络面临过拟合的问题。模型训练在第一轮训练后(不加正则化)性能迅速下降。传统的正则策略在面对稀疏输入和成千上万的参数时并不适用(比如l2和l1正则化)。
为此,提出小批量感知正则化,即只在每次小批量中对稀疏特征的参数计算$L_2-norm$。
$$L_2(W)=||W||_{2}^{2}$$
$$= \sum_{j = 1}^{K}||w_j||_{2}^{2}$$
$$= \sum_{(x,y)∈S}\sum_{j = 1}^{K}\frac{I(x_j≠0)}{n_j}||w_j||_2^2$$
$I(x_j≠0)$表示x有特征j,$n_j$表示特征id j出现的数量。上述公式可以被转换为下面的小批量感知形式:
$$L_2(W) = \sum_{j = 1}^{K}\sum_{m = 1}^{B}\sum_{(x,y)∈B_m}\frac{I(x_j≠0)}{n_j}||w_j||_2^2$$
其中,B表示小批量的数量,$B_m$表示第m次小批量。定义$α{mj} = max{(x,y)∈B_m}I(x_j ≠ 0)$为小批量$B_m$中至少有一次有特征id j。
上述近似为
$$L_2(W) ≈ \sum_{j = 1}^{K}\sum_{m = 1}^{B}\frac{α_{mj}}{n_j}||w_j||_2^2$$
通过这种方式,推导出了一种$l_2$正则化的近似小批量感知形式。
对于第m次小批量,关于特征j的嵌入权重的梯度为
$$w_j\leftarrow w_j - \eta[\frac{1}{|B_m|}\sum_{(x,y)∈B_m}\frac{\partial L(p(x), y)}{\partial w_j} + \lambda \frac{α_{mj}}{n_j}w_j]$$
在这里只有出现在第m次小批量的特征参数才会参与正则计算。
数据自适应激活函数 Data Adaptive Activation Function
PReLU是常用的激活函数。
如图所示,PReLU在0附近有一个固定的转折点,这对于每层不同分布的输入是不合适的。于是,本文设计了一个自适应激活函数Dice。
$$f(s) = p(s)·s + (1-p(s))·αs, p(s) = \frac{1}{1 + e^{-\frac{s-E[s]}{\sqrt{Var[s] + \epsilon}}}}$$
E[s]和Var[s]代表每次小批量输入的均值和方差。$\epsilon$是一个常量,此处设为$10^{-8}$。
Dice的主要思想是根据输入数据分布自适应调整转折点,值设置为输入的平均值。另外,Dice在两个函数间切换很顺滑。当E(s) = 0且Var[s] = 0时,Dice退化到PReLU。
实验 EXPERIMENTS
数据集和实验步骤 Datasets and Experimental Setup
数据集三个:Amazon Dataset, MovieLens Dataset和Alibaba Dataset。
Amazon Dataset:http://jmcauley.ucsd.edu/data/amazon/
MovieLens Dataset:https://grouplens.org/datasets/movielens/20m/
数据集情况如图。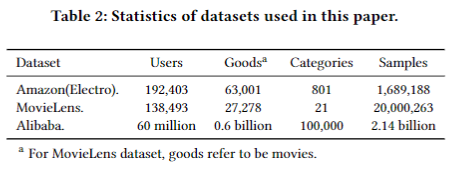
基线实验
- LR
- BaseModel
- Wide&Deep
- PNN
- DeepFM
策略
$$AUC = \frac{\sum_{i = 1}^{n}impression_i \times AUC_i}{\sum_{i = 1}^{n}impression_i}$$
$$RelaImpr = (\frac{AUC(measured model) - 0.5}{AUC(base model) - 0.5} - 1) \times 100\%$$
RelaImpr用来衡量模型间的相对提升。
亚马逊数据集和MovieLens数据集模型对比结果 Result from model comparison on Amazon Dataset and MovieLens Dataset
如图所示。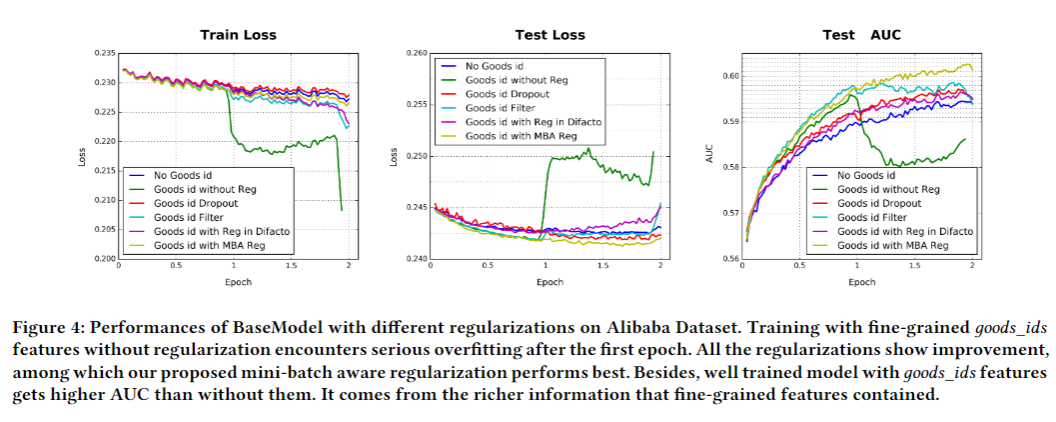
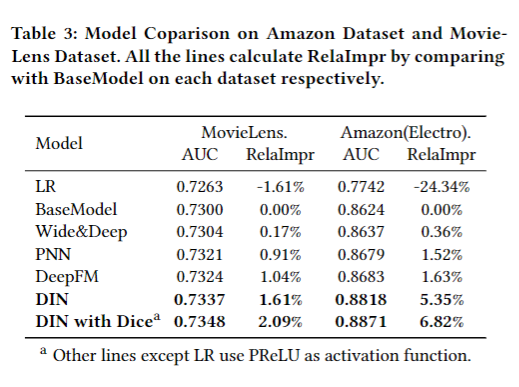
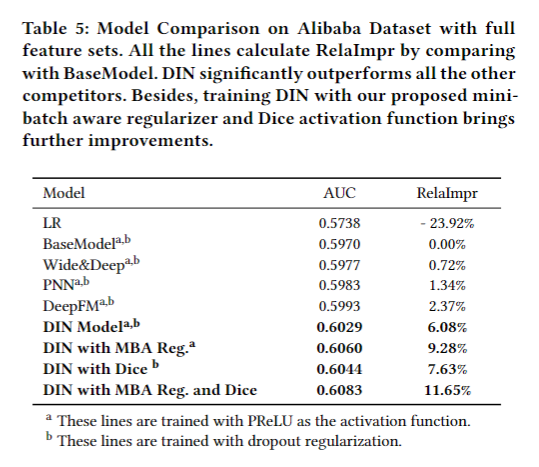
正则化性能 Performance of regularization
对比试验: